I’m starting up a machine learning framework and I’ve implemented k-means clustering for it.

I’m building KawaiiML to help me gain a better understanding of machine learning, such as how and why some of the algorithms work. I also want to slowly build and nurture an open source machine learning framework to aid others in their own machine learning endeavors, because I’m kind and noble. I’ve already written implementations for k-means clustering and gradient descent (which will be discussed in next week’s codex entry).

The source code repository for KawaiiML: https://github.com/webDva/KawaiiML

The following guides the reader through an implementation of the k-means clustering algorithm.

K-means clustering fundamentals

The objective of the k-means clustering technique is to find the set of means and clusters that yield the smallest intra-cluster variance as evidenced by [¹]

where $k$ is the number of clusters, $S$ the set of clusters, $x$ an observation that belongs to a particular cluster, and $\mu_i$ the mean of the observations for a particular cluster. The distance between an observation $x$ and a cluster’s center is given by $\|x - \mu_i\|^2$, which is the Euclidean distance squared between an observation and cluster’s center, or centroid, which is indeed given by the cluster’s mean $\mu_i$.

An algorithm for performing k-means clustering

The k-means clustering technique uses iterative refinement to alter observation-cluster memberships and cluster centroids as it endeavors to find its objective of the set of means and cluster groupings that yield the smallest intra-cluster variance.

The iterative refinement process consists of two steps:

1. The assignment of observations to clusters, or the expectation of observation-cluster memberships
2. The update of cluster centroids, or the maximization of cluster means

Once inter-cluster variance has been fully maximized, convergence will have been reached and the algorithm stops. The algorithm will have then yielded the set of means and observation-cluster pairs that satisfy the algorithm’s objective.

Initialization of cluster centroids

Prior to the iterative refinement process, a set of cluster centroids must be given. The initialization method that we will use in our implementation will simply consist of randomly selecting observations and using their values as the initial means.

Expectation step

The first step of each iteration of the process involves the assignment of individual observations to the cluster that is closest to them. Formally, at each iteration $t$, an observation $x_p$ is assigned to the cluster $S_i^{(t)}$ if the Euclidean distance squared between that cluster’s centroid $\mu_i^{(t)}$ and the observation is the smallest out of all the others.

The following helps show how observations are assigned.

Maximization step

Having determined groupings for all the observations, the means of all the clusters are modified to reflect these new observation-cluster memberships. For each cluster centroid $\mu_i^{(t)}$, a new cluster mean $\mu_i^{(t + 1)}$ is calculated by obtaining the mean of the observations in the cluster $S_i^{(t)}$.

Note that $|S_i^{(t)}|$ is the number of observations in the cluster.

Criterion for convergence

At the end of each iteration of the process, convergence will have been determined to have been reached when the updating of the cluster centroid means does not result in a change.

Implementation

Our particular implementation will use Python as the programming language and numpy for some of its conveniences, like normalizing the observation vectors and conveniently summing elements in a list.

import numpy

First, we design the function and its interface. The function that abstracts the implementation will simply be named kmeans. The function’s interface involves passing the set of observations as a numpy array and the number of clusters $k$ as an integer.

def kmeans(observations, k):

We want to track the number of iterations that occur, so we initialize a counter iterations to zero.

iterations = 0

Prior to engaging in the iterative refinement process, the algorithm initializes the first set of cluster means. It creates the list of means by randomly iterating through $k$ iterations and populating a list named cluster_means that will store the cluster centroids.

cluster_means = []
for i in range(k):
    cluster_means.append(numpy.random.choice(observations))

A loop that always executes at the top due to its True condition will be used as the iterator for the expectation-maximization process. The loop’s infinitely occurring execution ceases at the bottom of the loop block whenever convergence happens.

while True:
    iterations += 1 # used for tracking the number of iterations

On each expectation step, a list of empty lists clusters is created which will contain the observation-cluster memberships. Then, for each observation, it is considered the closest to the cluster centroid or mean whose Euclidean distance squared is the smallest. The observation is then added to the cluster’s list of observations.

clusters = [[] for i in range(k)]
for x in observations:
    closest_cluster_index = numpy.argmin([numpy.linalg.norm(x - mean) ** 2 for mean in cluster_means])
    clusters[closest_cluster_index].append(x)

The algorithm then maximizes the cluster means by calculating new means and adds them to a list new_cluster_means.

new_cluster_means = [[] for i in range(k)]
for mean in cluster_means:
    new_cluster_means[cluster_means.index(mean)] = numpy.sum(clusters[cluster_means.index(mean)]) / len(clusters[cluster_means.index(mean)])

Convergence is then checked for by determining if the new cluster means are identical to that of the previous iteration’s cluster means. If they are identical, then convergence will have been achieved and the algorithm terminates the iterative refinement process. If convergence has not yet been reached, then the algorithm proceeds to the next iteration after updating the cluster means with the new cluster means.

if new_cluster_means == cluster_means:
    break
cluster_means = new_cluster_means

Upon exiting from the last iteration, the function returns the results as a tuple containing the list of means, the cluster groupings, and the number of iterations it took.

return (cluster_means, clusters, iterations)

Full source code

import numpy

def kmeans(observations, k):
    iterations = 0

    cluster_means = []
    for i in range(k):
        cluster_means.append(numpy.random.choice(observations))

    while True:
        iterations += 1

        clusters = [[] for i in range(k)]
        for x in observations:
            closest_cluster_index = numpy.argmin([numpy.linalg.norm(x - mean) ** 2 for mean in cluster_means])
            clusters[closest_cluster_index].append(x)

        new_cluster_means = [[] for i in range(k)]
        for mean in cluster_means:
            new_cluster_means[cluster_means.index(mean)] = numpy.sum(clusters[cluster_means.index(mean)]) / len(clusters[cluster_means.index(mean)])

        if new_cluster_means == cluster_means:
            break
        cluster_means = new_cluster_means

    return (cluster_means, clusters, iterations)

Example of the implementation in action

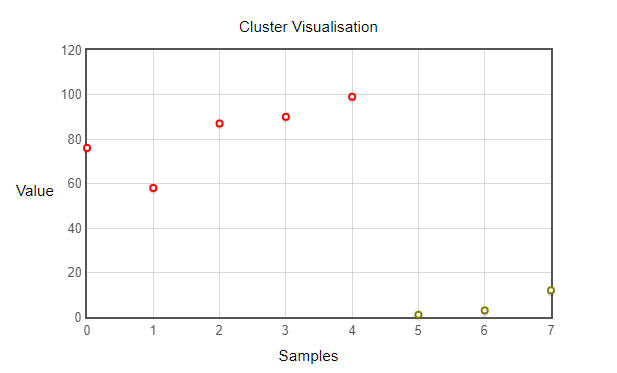
Providing the function with a set of values [76, 58, 87, 90, 99, 1, 3, 12] and $k = 2$, the function call looks like

kmeans(numpy.array([76, 58, 87, 90, 99, 1, 3, 12]), 2)

and returns a tuple like

([82, 5], [[76, 58, 87, 90, 99], [1, 3, 12]], 2)

Which is expected, considering [76, 58, 87, 90, 99] with a mean of 82 is different from [1, 3, 12] with a mean of 5. This difference is evidenced by the following visualization.

Conclusion

A consideration of this implementation is that it can only operate on vectors of one dimension. Also, the implementation’s initialization of the cluster means is flawed as there’s a chance that duplicate initial means could occur thereby affecting the final clustering. But for this guide’s purpose, the code used suffices. And I’m not going to mention the concept of local and global optimum regarding k-means clustering as neglecting to mention it also suffices for this guide.

I’ve come a long way from simple linear regression, and this codex entry has a similar pattern to my older simple linear regression entry.

But there is still much work that needs to be done.

Footnotes